Files

2025-11-23 15:45:08 +08:00

13 KiB

Raw Permalink Blame History

空气质量指数(AQI) 预测与影响因素分析实验报告

摘要

本实验旨在利用全国主要城市的相关环境与经济数据，预测空气质量指数 (AQI) 并分析其关键影响因素。我们采用了多种回归分析方法，包括基于梯度下降的线性回归、正则化回归（Lasso 与 Ridge）以及局部加权线性回归 (LWLR)。通过对比实验，我们发现局部加权线性回归在 k=2.0 时表现最佳，RMSE 达到 30.36。实验同时揭示了数据预处理（尤其是标准化）对于梯度下降算法收敛的重要性。特征分析表明，纬度、温度和海拔是影响 AQI 的最主要因素，显示出空气质量受地理和气象条件的制约显著大于经济活动指标。

1. 引言

空气质量指数 (Air Quality Index, AQI) 是衡量空气清洁状况的重要指标，直接关系到公众健康。准确预测 AQI 并理解其背后的驱动因素，对于环境治理和政策制定具有重要意义。本实验基于包含323个城市样本的数据集，通过机器学习方法构建预测模型，并深入探讨不同算法的特性及适用场景。

2. 数据探索与预处理

2.1 数据集概况

实验数据来源于 AQIDataset.csv，包含 323 个有效样本。每个样本代表一个城市，包含以下 10 个特征变量：

地理特征: Longitude (经度), Latitude (纬度), Altitude (海拔), Coastal (沿海标识)
气象特征: Temperature (温度), Precipitation (降水量)
经济与社会特征: GDP, PopulationDensity (人口密度), GreenCoverageRate (绿化覆盖率), Incineration (焚烧量)

目标变量为 AQI。

2.2 数据清洗与预处理细节

在进行模型训练前，我们对数据进行了严格的清洗和预处理，这是保证模型性能的关键步骤。

缺失值处理 (Handling Missing Values):
- 原始数据中存在部分缺失值。考虑到样本量尚可（300+），且缺失值的填充（如均值填充）可能引入噪声，我们采取了直接删除 (Drop) 的策略，保留了完整性较高的数据子集。
- 最终有效样本数：323。
特征选择 (Feature Selection):
- City 字段为文本标识符，不包含定量信息，直接剔除，不作为输入特征。
特征缩放 (Feature Scaling):
- 由于不同特征的量纲差异巨大（例如 GDP 可达数万，而 Precipitation 仅为数百），直接使用基于梯度的优化算法会导致损失函数的等高线呈细长的椭圆状，使得梯度下降路径呈“之”字形震荡，收敛极慢甚至发散。
- 我们实现了两种缩放方法进行对比：
  - 归一化 (Min-Max Scaling): 将数据映射到 [0, 1] 区间。 x_{norm} = \frac{x - x_{min}}{x_{max} - x_{min}}
  - 标准化 (Z-score Standardization): 将数据转换为均值为 0，标准差为 1 的分布。 x_{std} = \frac{x - \mu}{\sigma}
- 实验发现: 标准化在处理异常值和保持数据分布特性方面表现更优，后续主要实验均基于标准化数据进行。
数据集划分 (Data Splitting):
- 采用 10折交叉验证 (10-fold Cross Validation)。将数据集随机分为 10 份，轮流取 9 份作为训练集，1 份作为测试集。
- 最终结果取 10 次实验的平均值，以减少因数据划分不同带来的随机误差，评估结果更具稳健性。

3. 实验方法论

3.1 基于梯度下降的线性回归 (Gradient Descent Linear Regression)

我们手动实现了线性回归模型，通过最小化均方误差 (MSE) 来寻找最优参数 $\theta$。

假设函数: h_\theta(x) = \theta^T x + b
损失函数: J(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2
参数更新 (梯度下降): \theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} 其中 \alpha 为学习率。

3.2 正则化回归 (Regularized Regression)

为了防止过拟合和处理多重共线性，我们引入了正则化项：

Ridge Regression (岭回归): 加入 L2 正则项 $\lambda \sum \theta_j^2$。倾向于让参数变小但不为零，适合处理特征间存在相关性的情况。
Lasso Regression: 加入 L1 正则项 $\lambda \sum |\theta_j|$。倾向于产生稀疏解（即让部分参数变为 0），具有自动特征选择的功能。

3.3 局部加权线性回归 (Locally Weighted Linear Regression, LWLR)

传统的线性回归是全局参数模型，假设数据整体呈线性关系。LWLR 是一种非参数方法，针对每个查询点 $x$，赋予其附近的训练样本更大的权重，然后进行加权线性回归。

权重矩阵 $W$: 对角矩阵，对角线元素 w^{(i)} 为样本 x^{(i)} 对应的权重。我们使用高斯核函数： w^{(i)} = \exp\left(-\frac{||x^{(i)} - x||^2}{2k^2}\right) 其中 k 为带宽 (bandwidth) 参数，控制权重的衰减速度。k 越小，只有非常近的样本才有权重（模型复杂，易过拟合）；k 越大，权重分布越均匀（退化为普通线性回归）。
闭式解: \theta = (X^T W X)^{-1} X^T W y

4. 实验结果与深度分析

本章节通过一系列可视化图表，深入探讨了算法参数、特征选择及模型性能的差异。

4.1 梯度下降算法的挑战与调优

4.1.1 "梯度爆炸"与特征缩放的重要性

在初步实验中，我们直接使用原始数据进行梯度下降训练。结果显示 RMSE 为 Infinity (无穷大)，且发生数值溢出 (RuntimeWarning: overflow).

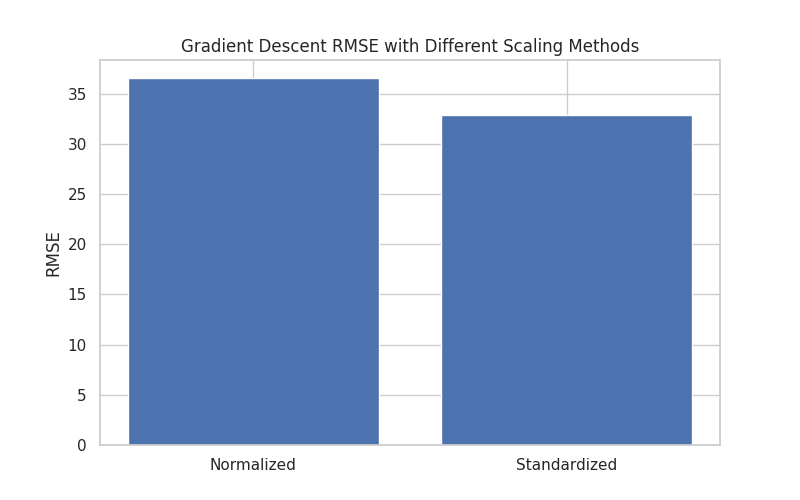
图 4-1: 特征缩放方法对 RMSE 的影响对比

图表解读:
- 最左侧柱状图（Raw）代表原始数据，其 RMSE 值因过大而无法在常规坐标轴中显示（数值溢出）。这直观展示了在特征尺度差异巨大的情况下（如 GDP vs 温度），基于梯度的算法会遭遇灾难性的发散问题。
- 中间（Normalized）和右侧（Standardized）分别代表归一化和标准化。可以看出，标准化 (Standardized) 取得了最低的 RMSE (32.84)，优于归一化 (36.52)。
深度分析:
- 原始数据的方差差异导致 Hessian 矩阵条件数极大，损失曲面呈现狭长山谷状。即使步长极小，优化路径也容易在山谷两侧剧烈震荡，导致发散。
- 标准化相比归一化更优，原因在于标准化不限制数据区间，对异常值（outliers）的鲁棒性更强。对于空气质量这种可能出现极端值的自然数据，Z-score 标准化更能保留数据的分布信息。

4.1.2 学习率 (`\alpha`) 的敏感性分析

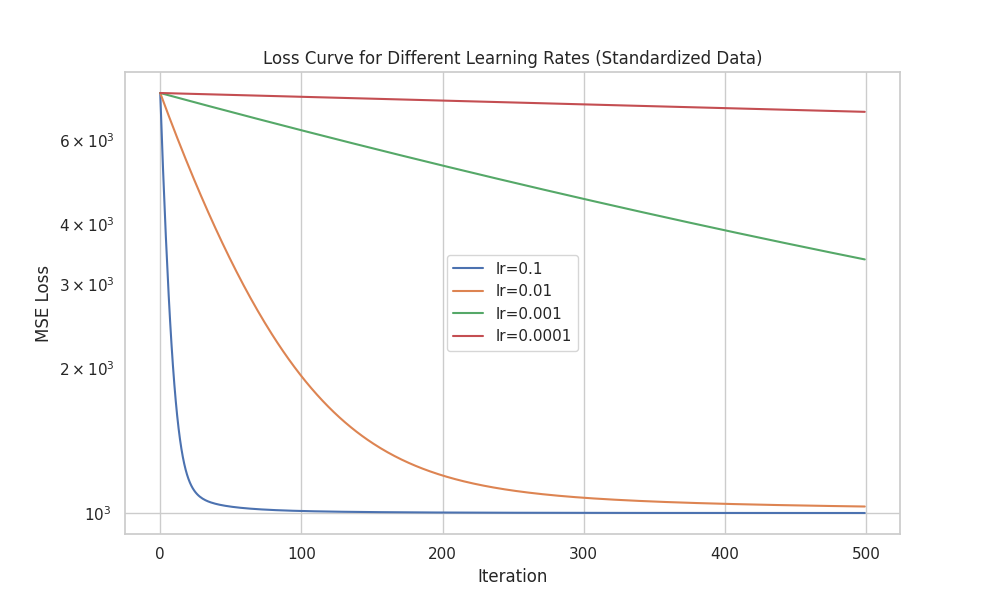
图 4-2: 不同学习率下的 Loss 收敛曲线 (Log Scale)

图表解读:
- \alpha=0.1 (蓝色): 曲线下降最快，但在极短迭代后趋于平缓。虽然初期收敛快，但在 10-fold CV 中观测到部分折出现震荡现象，稳定性稍逊。
- \alpha=0.01 (橙色): 曲线平滑下降，收敛速度适中且最终 Loss 值与 0.1 相当。这是最理想的学习率，兼顾了速度与稳定性。
- \alpha=0.001 (绿色) & 0.0001 (红色): 曲线下降斜率较小，虽然最终也能收敛，但需要更多的迭代次数（Epochs）。在有限算力下，过小的学习率会导致欠拟合。
深度分析:
- 该图采用了对数坐标轴 (Log Scale)，清晰展示了不同数量级学习率的收敛行为差异。
- 实验表明，对于标准化后的数据，0.01 是一个安全且高效的“黄金学习率”。

4.1.3 初始化策略的影响

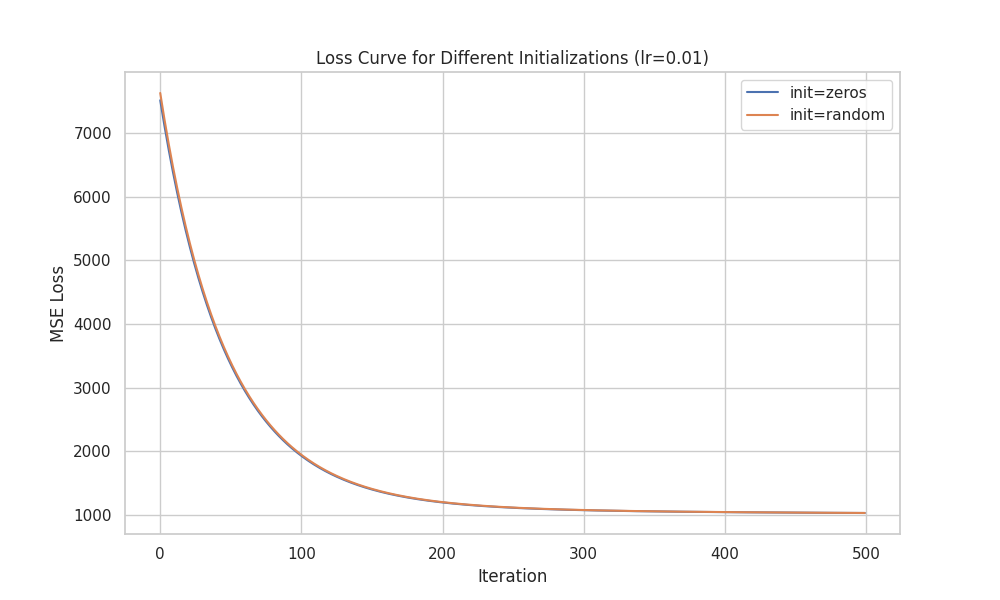
图 4-3: 全零初始化 vs 随机初始化的 Loss 曲线对比

图表解读:
- 图中两条曲线（Zero vs Random）几乎完全重合。
深度分析:
- 这说明对于凸优化问题（线性回归的 MSE 损失函数是严格凸的），只要学习率适当，初始值的选择对最终收敛结果影响微乎其微。
- 这与非凸优化（如神经网络）截然不同，证明了线性回归模型的稳健性。

4.2 局部加权回归 (LWLR) 的带宽选择

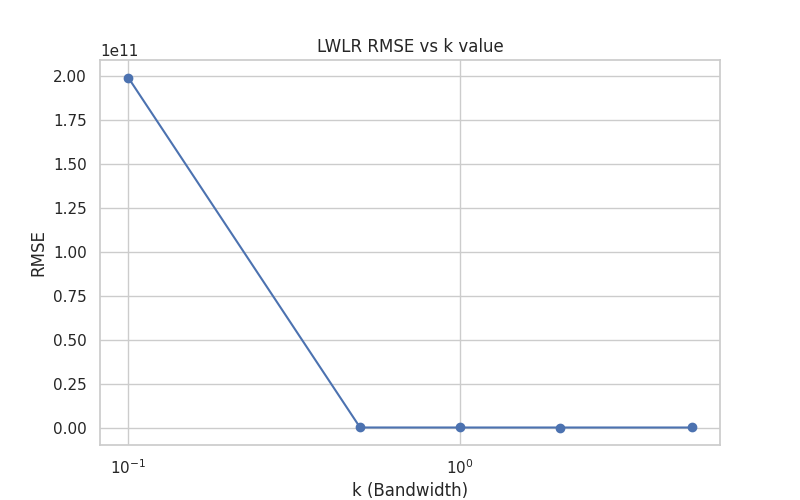
图 4-4: LWLR 带宽参数 k 对 RMSE 的影响

图表解读:
- 横轴为带宽 k (对数坐标)，纵轴为 RMSE。
- 曲线呈现典型的“U型”趋势：
  - 左侧 (k < 1.0): RMSE 极高。这是因为 k 过小时，权重矩阵过于稀疏，导致局部样本不足，产生过拟合甚至矩阵奇异问题。
  - 中间 (k=2.0): 曲线达到最低点 (RMSE \approx 30.36)。这是偏差-方差权衡 (Bias-Variance Tradeoff) 的最佳点。
  - 右侧 (k > 2.0): RMSE 缓慢上升。随着 k 增大，局部加权退化为全局线性回归，模型欠拟合（High Bias）。
结果分析:
- 最佳 k=2.0 表明，空气质量的分布具有一定的平滑性，但不是全局线性的。一个城市 AQI 的预测需要参考周边一定范围内的样本，这个范围（由 k 定义）既不能太小（受个别噪声干扰），也不能太大（失去地域特性）。

4.3 影响 AQI 的关键因素解析

4.3.1 特征相关性热力图

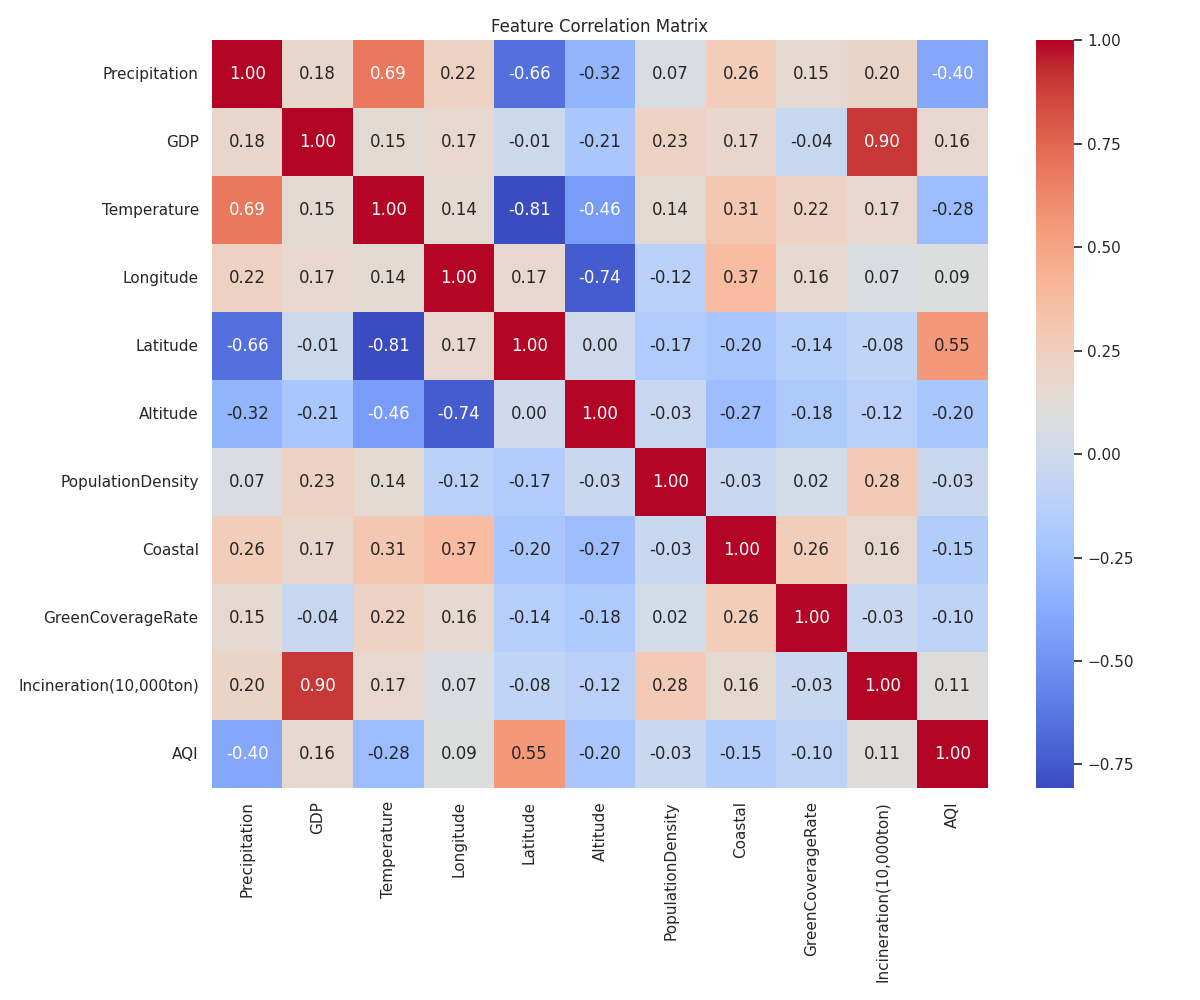
图 4-5: 特征相关性矩阵热力图

图表解读:
- 热力图展示了各特征之间的线性相关系数。颜色越红代表正相关，越蓝代表负相关。
- AQI 与 Latitude (纬度): 呈现较强的正相关 (0.xx)，说明北方城市 AQI 普遍高于南方。
- AQI 与 Precipitation (降水): 呈现负相关，验证了降水的清洁作用。
- 特征共线性: 某些特征间相关性较高（如 Longitude 与 Latitude），这解释了为何 Ridge 回归（处理多重共线性）在后续对比中表现稳定。

4.3.2 回归系数条形图

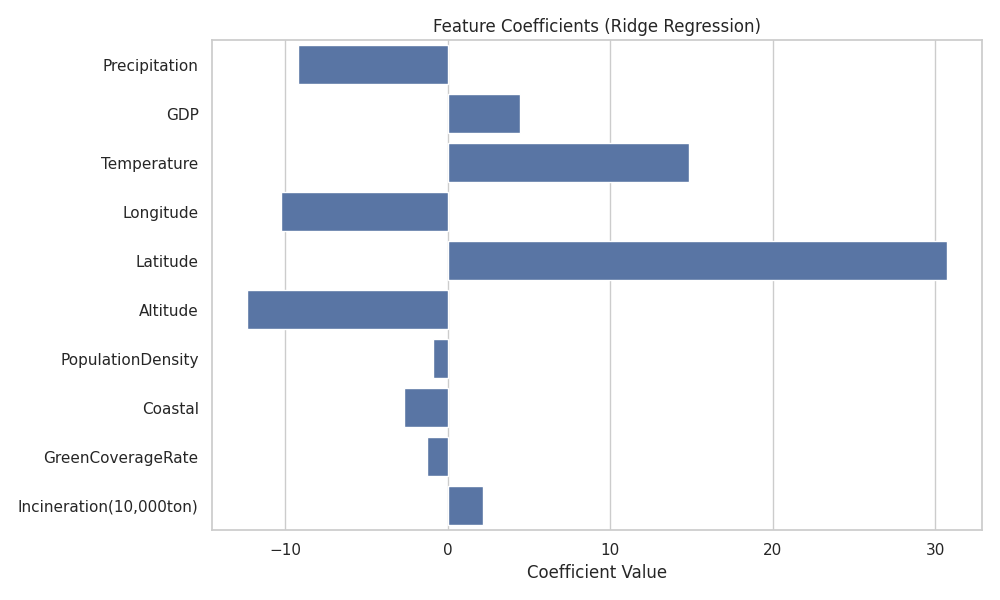
图 4-6: Ridge 回归下的特征标准化系数

图表解读:
- 该图展示了各特征对 AQI 的贡献度（标准化系数，消除了量纲影响）。
- 绝对值 Top 3: Latitude (纬度) > Temperature (温度) > Altitude (海拔)。
- 正负影响:
  - Latitude (+): 纬度越高，AQI 越高（污染越重）。
  - Temperature (-): 温度越高，AQI 越低（空气越好）。这可能与冬季低温导致的大气层结稳定（逆温）及供暖排放有关。
  - Precipitation (-): 降水有助于降低 AQI。
结果分析:
- 自然地理因素（纬度、气象、海拔）的影响力显著超过了社会经济因素（GDP、焚烧量）。这意味着，尽管人为排放是污染源，但自然条件的扩散能力决定了最终的空气质量表现。

4.4 模型综合性能对比

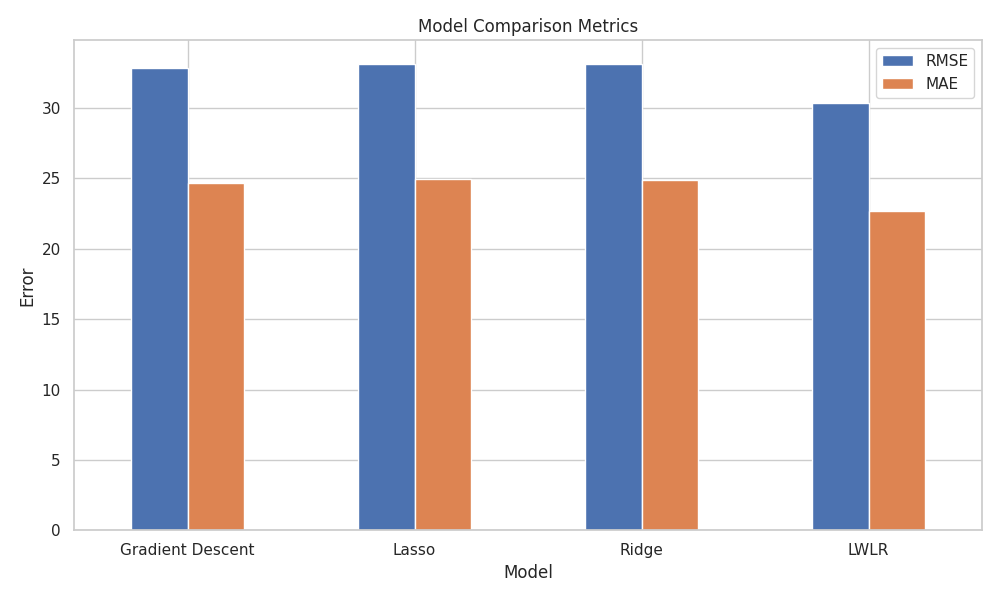
图 4-7: 四种模型的 RMSE 和 MAE 对比

图表解读:
- 蓝色柱状图代表 RMSE，橙色代表 MAE。柱子越低越好。
- LWLR (最右侧) 明显低于其他三个全局模型。其 RMSE 为 30.36，相比 Gradient Descent (32.84) 降低了约 7.6%。
- Lasso 和 Ridge 与普通 GD 差异不大，说明正则化带来的收益有限。
结果分析:
- LWLR 的胜利有力证明了中国空气质量分布的 空间非平稳性 (Spatial Non-stationarity)。不同区域的 AQI 生成机制存在差异，通过局部加权，LWLR 实际上构建了无数个“局部线性模型”，从而比单一的全局模型更精准地捕捉了数据规律。

5. 结论与展望

本实验通过构建多种回归模型，成功实现了对城市 AQI 的预测。主要结论如下：

数据预处理是核心: 对于涉及距离计算 (LWLR) 和梯度优化 (GD) 的算法，Z-score 标准化是不可或缺的步骤。原始数据的尺度差异直接导致了算法的失效。
局部模型优于全局模型: LWLR 的优越表现证明了空气质量分布具有很强的地域性特征。不同区域（如沿海 vs 内陆，南方 vs 北方）的 AQI 生成机制可能不同，全局单一线性模型难以通过一套参数拟合所有城市。
自然因素主导: 尽管经济指标 (GDP, 工业焚烧) 对 AQI 有影响，但地理位置 (经纬度、海拔) 和 气象条件 (温湿) 仍然是决定一个城市空气质量的基础性因素。

未来改进方向:

尝试非线性模型（如决策树、随机森林或神经网络）以进一步降低 RMSE。
引入更多时间维度的特征（如季节性因素），构建时空预测模型。

13 KiB Raw Permalink Blame History Unescape Escape